Recurrent Neuro Network
循环神经网络可以更好地处理序列信息(如一句话),允许记忆信息(在时序上传递输入的有效信息),可以解决长期依赖的问题(Long-term Dependencies)
RNN结构
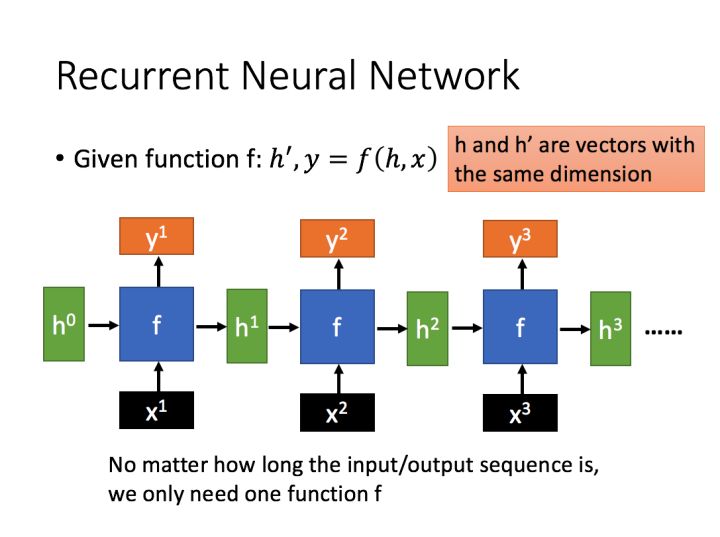
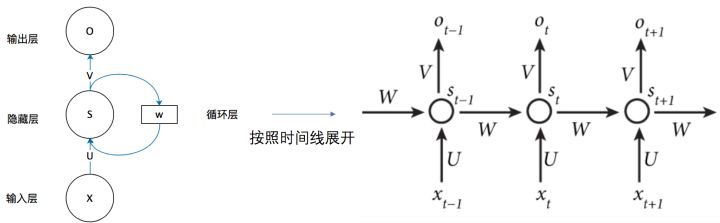
$$O_t = g(VS_t)$$ # 在时间点 t 的输出
$$S_t = f(UX_t + WS_{t-1})$$ # 在时间点 t 的状态
W,V,U: 权重
g,f: 激活函数

循环
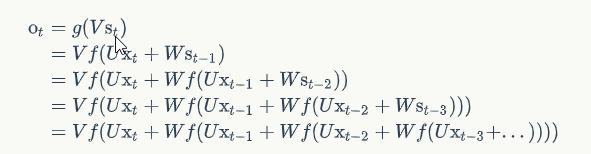
输出值 $O_t$ 受前面历次输入值 $x_t, x_{t-1}, x_{t-2}…$ 的影响,相当于一定程度上记忆之前任意时间段的有效信息,从而在时序上累积输入 $X_t$,解决长期依赖问题。
疑问: S作为一个固定大小的矩阵如何记忆有效信息?
BPTT
损失函数对权重 $W$ 的梯度是各个时刻梯度之和:
$$\nabla_W L = \sum_{i=1}^{t} \nabla_{W_i} L$$
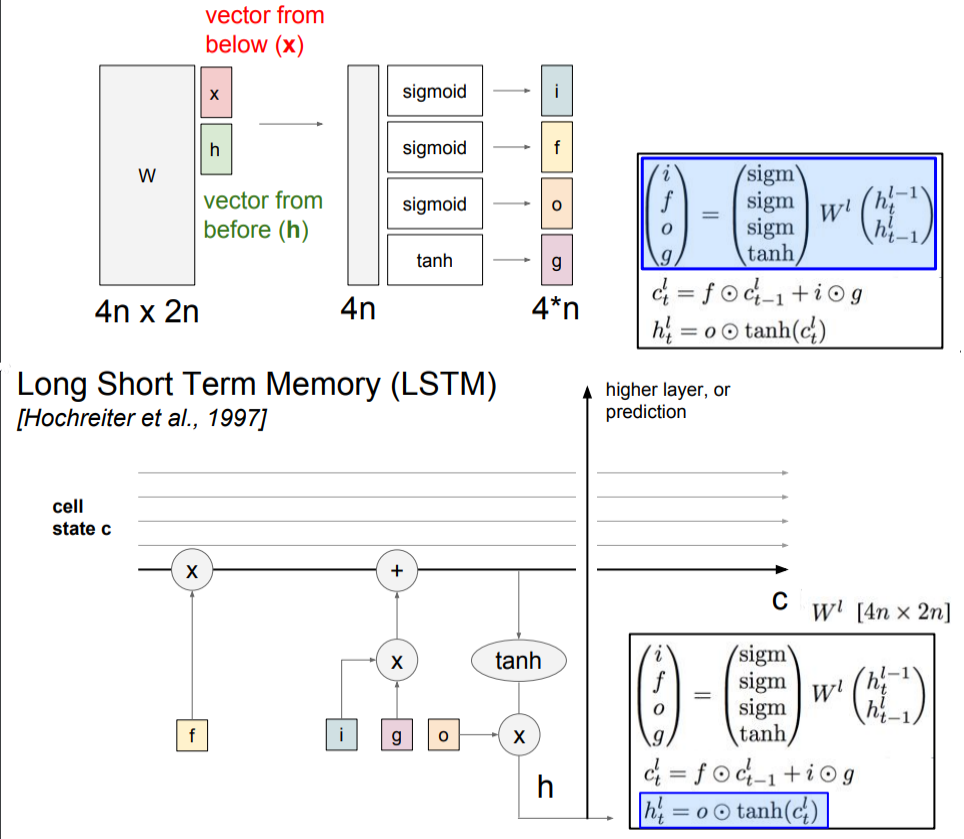
LSTM
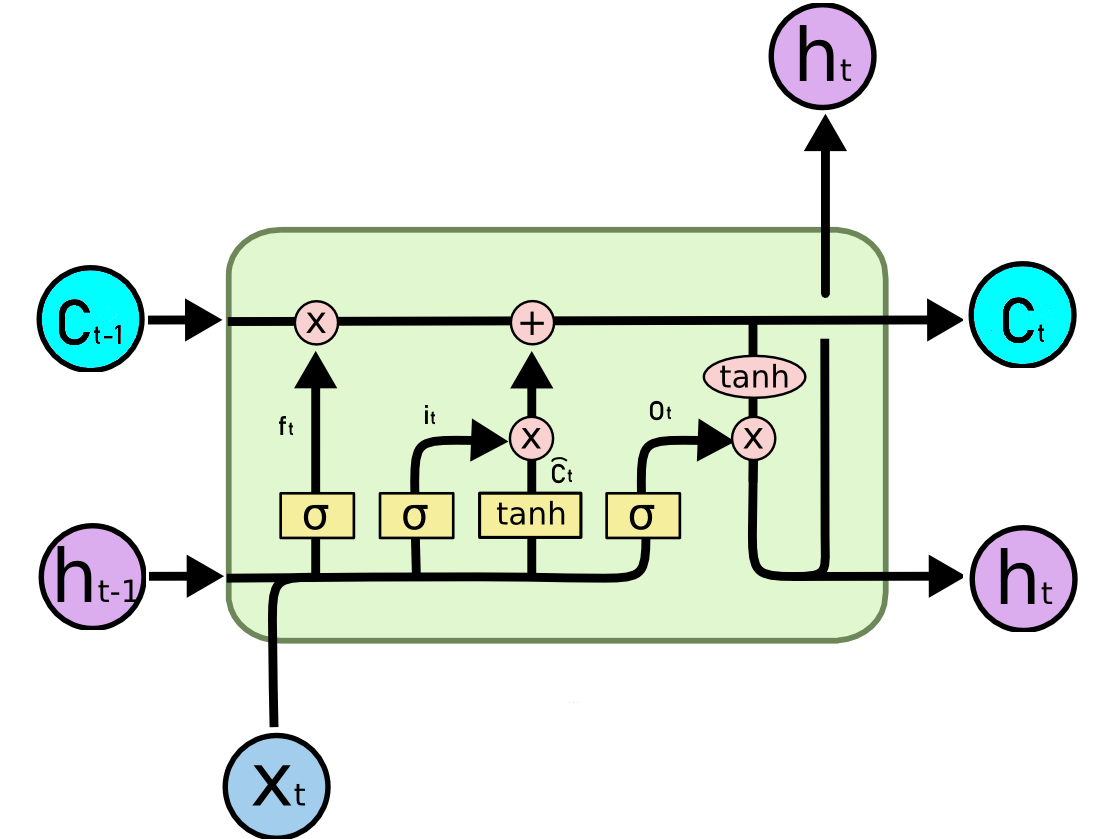
$$f_t = \sigma(W_f[h_{t-1}, x_t] + b_f) $$ # forget 遗忘门
$$i_t = \sigma(W_i[h_{t-1}, x_t] + b_i)$$ # input 输入门
$$\widetilde{C}_t = tanh(W_c[h_{t-1}, x_t] + b_c)$$ # 特征输入
<<<<<<< HEAD
=======
66f037c2f6c4b40611583b218ec6441bb47385a7
$$C_t = f_t \odot C_{t-1} + i_t \odot \widetilde{C}_t$$ # 选择性遗忘,选择性更新
$$h_t = o \odot tanh(C_t)$$ # output 输出门
GRU
合并遗忘门和输入门,使用$z_t$

References: