Neuron Network

深度学习和神经网络(CS231n Note)

深度学习和神经网络(CS231n Note)
1. 神经元模型与数学模型（Neuron Network Unit）
2. 常用激活函数
- sigmoid
- tanh
- relu
- Leaky Relu
- ELU
- Maxout
3. 数据预处理
4. 权重初始化
5. 正则化
- L1 正则
- L2正则

1. 神经元模型与数学模型（Neuron Network Unit）

大脑的基本计算单位是神经元（neuron）。人类的神经系统中大约有860亿个神经元，它们被大约$10^{14}-10^{15}$个突触（synapses）连接起来。下面图表的左边展示了一个生物学的神经元，右边展示了一个常用的数学模型。每个神经元都从它的树突获得输入信号，然后沿着它唯一的轴突（axon）产生输出信号。轴突在末端会逐渐分枝，通过突触和其他神经元的树突相连。

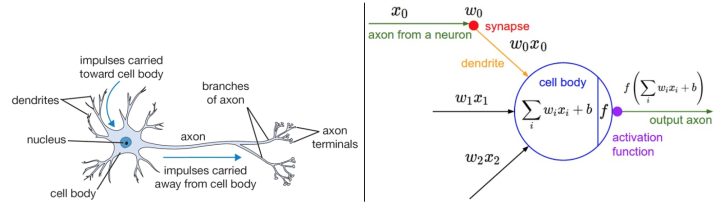
神经元（Neuron）通过树突（Dendrites）接收输入信号，沿着轴突（axon）产生输出信号。轴突在末端分叉，通过突触和其他神经元的树突相连。

输入信号（$x_0,x_1,…,x_n$）传递到其他神经元的树突，基于突触的突触强度相乘（$w_0x_0,w_1x_1,…,w_nx_n$）。突触的强度（权重$w$）可以控制一个神经元对另一个神经元的影响强度，使其兴奋（正权重）或抑制（负权重）。输出信号如果高于阈值，则神经元激活（对应于激活函数$f(\sum_{i}w_ix_i+b)$）。

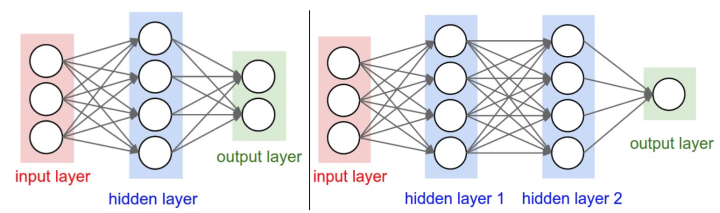
1 多层感知机

输入层 -> 隐藏层 -> 输出层

2. 常用激活函数

	函数	值域	导数	备注
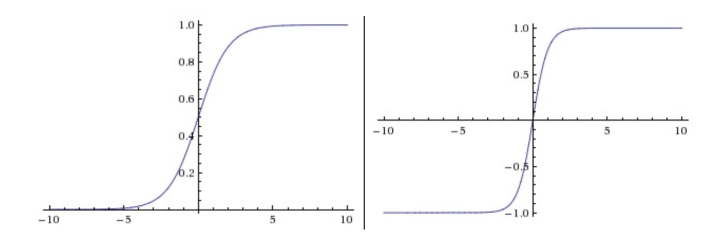
sigmoid	$ \sigma(x)=\frac{1}{1+e^{-x}} $	[0,1]	[0, 0.25] $\sigma’(x)=\sigma(x)(1-\sigma(x))$	分类概率
tanh	$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$	[-1,1]	[0, 1] $tanh’(x)=1-(tan(x))^2$
relu	$relu(x)=max(0, x)$	$[0,+\infty]$	$f’_x=\begin{cases}0, x<0 \\="" 1,="" x="">0 \ undefinded, x=0 \end{cases}$

sigmoid

优点：

分类概率

缺点

梯度容易饱和而丢失，激活函数在接近0,1时会饱和，如果权重过大，很容易失去梯度
函数不经过0，不以0点对称，在中间点0.5附近的的梯度较小（0.25），梯度总体较小，不利于梯度传播
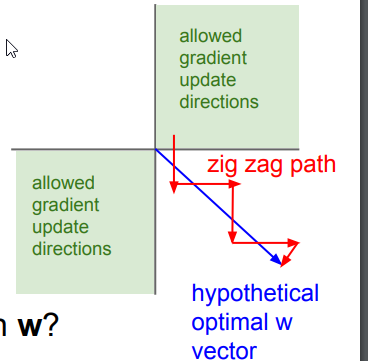
激活值永远全为正（负），下一神经元的输入总是正数（负数），则反向传播过程中梯度更新呈z字型
exp指数函数计算复杂

1560776135809

tanh

$tanh(x)=2\sigma(2x)-1$

优点：

范围更大 [0, 1]
以 0 为中心点
中间部分梯度更大，有利于梯度传播

缺点：

梯度饱和而丢失的情况仍然存在

relu

优点

收敛速度更快（e.g. 6x than sigmoid/tanh)
计算简单
梯度不会饱和

缺点

可能导致部分神经元“死掉”，永远不会被激活。输出值始终为负，激活值为0，梯度为0，反向传播不更新此神经元的梯度。降低学习率来降低神经元“死掉”的概率。

677187e96671a4cac9c95352743b3806_hd

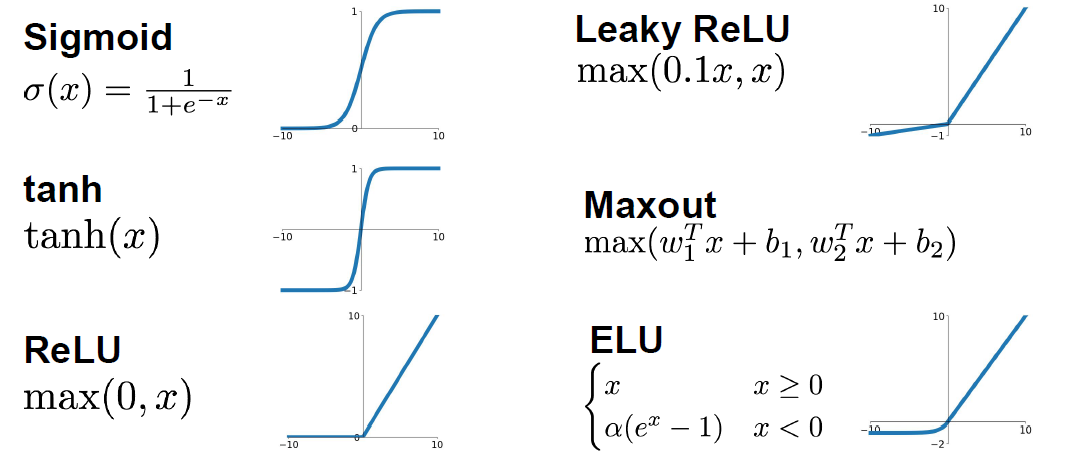
Leaky Relu

解决Relu死亡的问题

$$f(x)=\begin{cases}x, x>0\\alpha x, x<0\end{cases}$$, $\alpha=0.01$

ELU

$$f(x)=\begin{cases} x, x>0\ \alpha(e^x-1), x\leq0\end{cases}$$

1560776449074

Maxout

$$max(w_{1}^Tx+b_1, w_{2}^Tx+b_2)$$

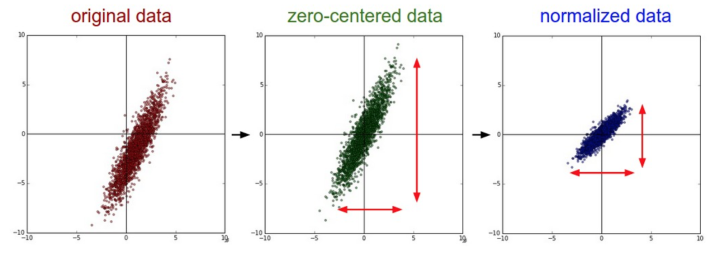
3. 数据预处理

归一化 Normalization

# 数据归一化
X = X / np.std(X, axis=0)
# 维度归一化
X = X / np.std(X, axis=1)

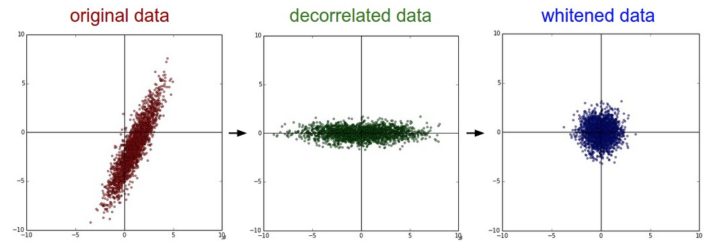
PCA 白化（很少在深度学习中使用）

PCA/白化。左边是二维的原始数据。中间：经过PCA操作的数据。可以看出数据首先是零中心的，然后变换到了数据协方差矩阵的基准轴上。这样就对数据进行了解相关（协方差矩阵变成对角阵）。右边：每个维度都被特征值调整数值范围，将数据协方差矩阵变为单位矩阵。从几何上看，就是对数据在各个方向上拉伸压缩，使之变成服从高斯分布的一个数据点分布。

CIFAR 数据PCA

nx3072 维向量（图片32x32x3）,协方差矩阵：3072x3072

1: 49张图片。2: 3072个特征值向量中的前144个。3: 49张PCA降维的图片（U.transpose()[:144,:]）。4: 白化后的数据。144个维度的方差都压缩到相同的数值范围（U.transpose()[:144,:]）。现在较低的频率（代表了大多数方差）可以忽略不计了，较高的频率（代表相对少的方差）就被夸大了。

4. 权重初始化

小随机数初始化

基于均值为0，标准差为1的高斯分布

1	W = 0.01 * np.random.randn(N, D)

使用$\frac{1}{\sqrt{n}} $校准方差

数据量增大，随机初始化的神经元输出数据分布的方差也增大

1	W = np.random.randn(N, D) / np.sqrt(N)

He Normal

网络中神经元的方差应该是$\frac{2}{n}$

当前的推荐是使用ReLU激活函数，并且使用w = np.random.randn(n) * sqrt(2.0/n)来进行权重初始化

1	W = np.random.randn(n) * sqrt(2.0/n)

偏置初始化 biases

1	b = np.zeros(n,)

5. 正则化

L1 正则

L2正则

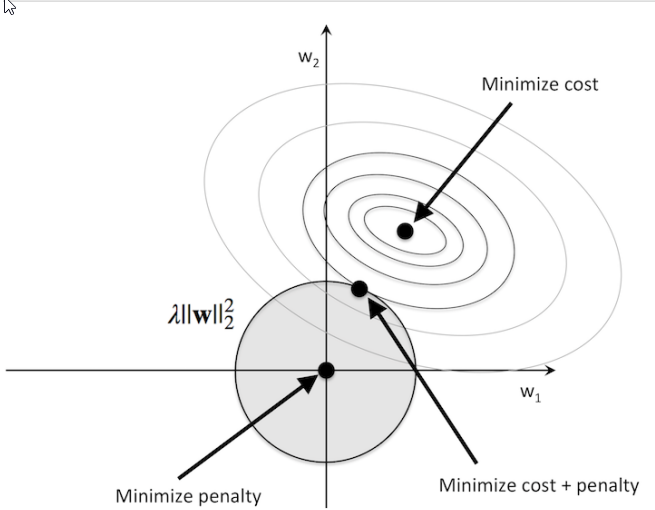
1561037588255

References: