信息量
信息量是对事件发生概率的度量
$log\frac{1}{p}$
一个事件发生的概率越低,则这个事件包含的信息量越大,比如说越稀奇新闻包含的信息量越大,因为这种新闻出现的概率低。
引用:一本五十万字的中文书平均有多少信息量?($\log_2m$) 《数学之美 - 吴军》
我们知道常用的汉字(一级二级国标)大约有 7000 字。假如每个字等概率,那么我们大约需要 13 个比特(即 13 位二进制数)表示一个汉字[这里把汉字作为一个随机变量,那么汉字系统的熵就是约13bit] 。但汉字的使用是不平衡的。实际上,前 10% 的汉字占文本的 95% 以上。因此,即使不考虑上下文的相关性,而只考虑每个汉字的独立的概率,那么,每个汉字的信息熵大约也只有 8-9 个比特。如果我们再考虑上下文相关性,每个汉字的信息熵[其实指的是汉字变量取特定汉字作为值时候具有的信息量] 只有5比特左右。所以,一本五十万字的中文书,信息量大约是 250 万比特[这个时候的信息量就是每个汉字的信息量和数目相乘,指的都是汉字变量取具体值的信息量] 。如果用一个好的算法压缩一下,整本书可以存成一个 320KB 的文件。如果我们直接用两字节的国标编码存储这本书,大约需要 1MB 大小,是压缩文件的三倍。这两个数量的差距,在信息论中称作“冗余度”(redundancy)。 需要指出的是我们这里讲的 250 万比特是个平均数,同样长度的书,所含的信息量可以差很多。如果一本书重复的内容很多,它的信息量就小,冗余度就大。
熵(Entropy)
信息论中,熵是接收每条消息中包含的信息量($\log\frac{1}{p}$)的平均值。
熵定义为信息的期望值(香农 shannon):
$$\begin{align} H(X) & = E[I(X)] \ & = E[log(\frac{1}{P(X)})] \ & = -\sum\limits_{i}^n P(x_i)logP(x_i)\end{align} $$
表示样本的不确定性量度。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
单位:
熵的单位通常为比特, bit 或者sh(annon) (基于2),但也用nat(基于自然对数)、Hart(基于10)计量,取决于定义用到对数的底。
- 离散均匀分布
$H(X)=log_2{m}$
例:抛掷三枚硬币
信息量:可以得到$2^3=8$种情况
不确定性:$log_2{8}=3\ bit$
- 离散分布
$H(X)=\sum\limits_{i}^nP(x_i)log\frac{1}{P(x_i)}$
例:选项ABCD
信息量:$H(X)=\sum\limits_{i}^n\frac{1}{4}log_2(\frac{1}{4})=2 bit$
给定A是错的,信息量变为:$H(X)=\sum\limits_{i}^n\frac{1}{3}log_2(\frac{1}{3})=1.585 bit$
“A是错的”,提供了$2-1.585=0.415bit$的信息
例:编码
分布p=(1/2, 1/2, 0, 0),即A和B出现的概率均为1/2,C和D出现的概率都为0。计算H(p)为1,即只需要1位编码即可识别A和B
分布q=(1/4, 1/4, 1/4, 1/4)来编码则得到H(q)=2,即需要2位编码来识别A和B,还有C和D
交叉熵
使用分布 q 来预测真实分布 p 的平均编码长度
$H(p,q)= E_p[\log \frac{1}{q(i)}] = \sum\limits_{i}^{} p(i)*log\frac{1}{q(i)} $
交叉熵可以看作每个信息片段在错误分布 q 下的期望编码位长度,而信息实际分布为 p。
现有关于样本集的2个概率分布p和q,其中p为真实分布,q预测分布。
按照真实分布p来衡量识别一个样本的所需要的编码长度的期望(即平均编码长度)为:$H(p)=\sum\limits_{i}^{} p(i)*log\frac{1}{p(i)}$
使用预测分布q来表示来自真实分布p的平均编码长度,则应该是:$H(p,q)=\sum\limits_{i}^{} p(i)*log\frac{1}{q(i)} $
因为用q来编码的样本来自实际分布p,所以期望H(p,q)中概率是p(i)。H(p,q)我们称之为“交叉熵”。
比如含有4个字母(A,B,C,D)的数据集中,真实分布p=(1/2, 1/2, 0, 0),即A和B出现的概率均为1/2,C和D出现的概率都为0,计算H(p)为1,即只需要1位编码即可识别A和B。如果使用分布Q=(1/4, 1/4, 1/4, 1/4)来编码则得到H(p,q)=2,即需要2位编码来识别A和B(C和D并不会出现)。
根据非真实分布q得到的平均编码长度H(p,q)大于根据真实分布p得到的平均编码长度H(p)。事实上,根据Gibbs’ inequality可知,H(p,q)>=H(p)恒成立,当q为真实分布p时取等号。
KL散度(相对熵)
衡量分布 p 和 q 的差异,使用分布 q 来近似分布 p $D_{KL}(p||q) \ge 0$
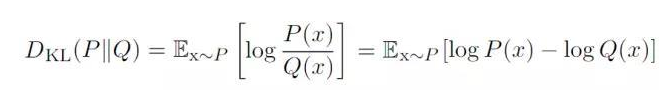
$D_{KL}(p||q)=E_{x ~ p}[\frac{\log p(i)}{\log q(i)}]=H(p,q)-H(p) = \sum\limits_{i}^{} p(i)\log\frac{1}{q(i)} - \sum\limits_{i}^{} p(i) \log\frac{1}{p(i)} = \sum\limits_{i}^{} p(i)*\log\frac{p(i)}{q(i)}$
我们将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数称为“相对熵”,又被称为KL散度(Kullback–Leibler divergence,KLD) Kullback–Leibler divergence。它表示2个函数或概率分布的差异性:差异越大则相对熵越大,差异越小则相对熵越小,二者分布相同则相对熵为0。
可以得到,交叉熵 $H(p,q)= E_p[\log \frac{1}{q(i)}] = H(p) + D_{KL}(p||q)$
其中 $H(p)$ 是 $p$ 的熵,$D_{KL}(p|q)$ 是从 $p$ 到 $q$ 的KL散度(也被称为p相对于q的相对熵)。
通常“相对熵”也可称为“交叉熵”,因为真实分布p是固定的,D(p||q)由H(p,q)决定。当然也有特殊情况,彼时2者须区别对待。
交叉熵作为损失函数
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。
交叉熵和均方误差都可以作为神经网络的损失函数,他们的区别在于:
- 交叉熵适用于分类问题,结果是离散的类别(如图片分类),而均方误差适用于回归问题,结果是一个连续的数值(如雨量预测)【实际上均方误差也可以用于分类问题】
- 在使用 sigmod 激活函数时,如果使用均方误差作为损失函数,反向传播的导数(直接影响学习速度)会包含 sigmod函数的梯度,这个梯度随着变量的增大会趋向于0,导致学习速度迅速降低(梯度消失);而如果使用交叉熵作为损失函数,就不存在这个问题,反向传播的导数包含 sigmod 函数,而不包含 sigmod 函数的导数。
1 | # softmax_cross_entropy_with_logits计算后,矩阵的每一行数据计算出一个交叉熵,三行数据共计算出三个交叉熵 |
References: